Адрес этой страницы' ?>

<<Предыдущая страница Оглавление книги Следующая страница>>

§ 2. СЛОЖЕНИЕ И РАЗЛОЖЕНИЕ СИЛ

Ниже приведены основные определения и положения, которыми пользуются при решении задач на сложение и разложение сил.

Система сил — совокупность сил, приложенных к телу.

Сходящиеся силы — силы, линии действия которых пересекаются в одной точке.

Равнодействующая — сила, заменяющая действие системы сил.

Сложить силы — значит найти их равнодействующую.

Разложить силу — значит найти ее составляющие. Две равные силы, направленные по одной прямой в противоположные стороны, взаимно уравновешиваются, тело при действии этих сил находится в равновесии, т. е. в состоянии покоя.

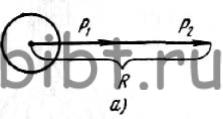
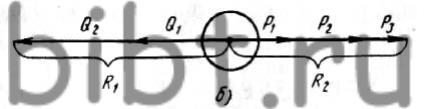
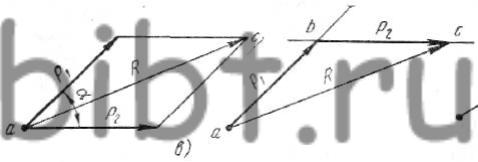
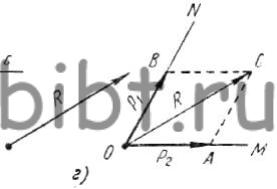
Рис. 54. Сложение и разложение сил:

сложение сил: а — направленных в одну сторону, б — направленных в противоположные стороны, в — направленных под углом; г — разложение силы на составляющие по заданным направлениям

Точку приложения силы, действующей на твердое тело, можно переносить по линии ее действия в любую другую точку, при этом действие силы не изменится.

Равнодействующая двух сил, приложенных под углом в одной точке, проходит через ту же точку и направлена по диагонали параллелограмма, построенного на этих силах.

Действие равно и противоположно противодействию.

Несвободное тело под действием сил оказывает на опору давление, которое равно и противоположно давлению, оказываемому опорой на тело.

Направление сил, действующих вправо и вверх, принято обозначать знаком плюс, а сил, действующих влево и вниз, — знаком минус.

Направление сил со знаком плюс считают положительным, а направление со знаком минус — отрицательным.

Сложение сил, действующих по одной прямой. Если силы действуют на тело по одной прямой и в одном направлении, то равнодействующая их R равна их сумме (рис. 54, а): R = P₁ + P₂. (11)

Если силы действуют на тело по одной прямой, но в разных направлениях, то равнодействующая их R равна алгебраической сумме этих сил. Для получения этой суммы надо из равнодействующей R₂ положительно направленных сил вычесть равнодействующую R₁ отрицательно направленных сил (рис. 54, б), т. е.

R₁ = Q₁ + Q₂; R₂ = P₁ + P₂ + P₃; R = R₂-R₁ (12)

Если равнодействующая этих сил равна нулю, то силы находятся в равновесии.

Пример. Q₂=40 кГ; Q₁ = 30 кГ; P₁=20 кГ; Р₂=25 кГ; и Р₃ =10 кГ (см. рис. 54, б). Равнодействующая R₁ отрицательно направленных сил равна 70 кГ (40+30), а равнодействующая R₂ положительно направленных сил равна 55 кГ (20+25+10). Общая равнодействующая R=55-70= -15 кГ. Величина R отрицательная — равнодействующая направлена влево.

Сложение и разложение сил, пересекающихся в одной точке. Равнодействующая R двух сходящихся сил по величине и направлению является диагональю параллелограмма, построенного на этих силах (рис. 54, в).

Таким образом, если на точку а действуют под углом α две силы P₁ и Р₂, то равнодействующая их по величине и направлению равна диагонали ас; направление равнодействующей от точки а к точке с.

Но для нахождения равнодействующей строить весь параллелограмм не обязательно, достаточно построить треугольник abc (см. рис. 54, в, справа). От точки а проводим линию, параллельную силе Р₁, на которой откладываем от точки а величину силы P₁ в выбранном масштабе (отрезок ab), через точку b проводим линию, параллельную силе Р₂, и откладываем на ней от точки b величину силы Р₂ в том же масштабе (отрезок bc). Соединив точки а и с прямой, получим треугольник abc. Линия ас будет являться равнодействующей R сил P₁ и Р₂. Равнодействующая направлена от точки а к точке с. Полученный треугольник abc представляет половину параллелограмма и называется треугольником сил.

Применяя правило параллелограмма или треугольника, легко найти равнодействующую любого числа сходящихся сил.

Разложение силы на две составляющие. Для разложения силы R на две составляющие, направление которых известно, эту силу принимают за диагональ параллелограмма сил, на которой строят параллелограмм или треугольник (в последнем случае сила будет являться третьей стороной треугольника). Стороны параллелограмма (или треугольника) будут являться искомыми составляющими силами.

Через точку С (рис. 54, г) проводим линию АС, параллельную ON, до встречи с линией ОМ в точке А и через ту же точку С проводим линию ВС, параллельную ОМ, до встречи с линией ON в точке В. Отрезки ОВ и ОА являются искомыми силами P₁ и Р₂.