
| Главная |
| Поиск по сайту |
Адрес этой страницы' ?>
Предыдущая Оглавление книги Следующая
Глава I
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАСЧЕТА ТЕХНОЛОГИИ ШТАМПОВКИ
1. Деформации и напряжения
Характерной особенностью всех операций штамповки является то, что они сопровождаются пластической (необратимой) деформацией, величина которой значительно превышает упругую деформацию, определяемую законом Гука:
ε=σт/E, где σт— предел текучести, E — модуль упругости.
Максимальная величина упругой деформации составляет десятые доли процента, в то время как формообразующие операции штамповки вызывают изменение первоначальных размеров заготовки в пределах 10—20% и более, а на разделительных операциях штамповки пластические деформации достигают еще большей величины равной предельным значениям, соответствующим разрушению материала.
Штампуемый материал оказывает сопротивление пластическому деформированию, и возникающие при этом напряжения в отдельных сечениях заготовки превосходят величину напряжения в зоне упругих деформаций.
При анализе характера и интенсивности
происшедшего формоизменения заготовки в отдельных ее сечениях
устанавливается не величина абсолютного изменения длины отрезка,
соединяющего какие-нибудь две произвольные материальные точки, а
величина отношения приращения длины этого отрезка к самой длине, т.
е. относительное удлинение или укорочение. Отрезок l0 может
изменяться при упругой деформации заготовки весьма мало, а при его
пластической деформации значительно (конечно). В последнем случае для
определения происшедшей деформации известные выражения, применяемые в
сопротивлении материалов упругим деформациям, ![]() оказываются
неприемлемыми, так как они либо завышают, либо занижают результат.
Поэтому вывод формулы расчета относительных конечных деформаций,
обеспечивающей их истинное значение, производится по методу Г. А.
Смирнова-Аляева [11, 12]. Пусть в процессе преобразования отрезка l0 до
значения l он
принимает ряд промежуточных значений: l0;l1;l2;l3;...;li;li+1;...;ln-1;ln, где ln=l.
оказываются
неприемлемыми, так как они либо завышают, либо занижают результат.
Поэтому вывод формулы расчета относительных конечных деформаций,
обеспечивающей их истинное значение, производится по методу Г. А.
Смирнова-Аляева [11, 12]. Пусть в процессе преобразования отрезка l0 до
значения l он
принимает ряд промежуточных значений: l0;l1;l2;l3;...;li;li+1;...;ln-1;ln, где ln=l.
Полагая разность двух смежных значений
переменной в процессе деформации длины отрезка малой по сравнению с
этой длиной в данный момент ее преобразования, т.е. считая ![]() за
величину, малую по сравнению с единицей, можно представить
результативную деформацию при изменении длины от l0 до ln как
сумму последовательных малых относительных деформаций
за
величину, малую по сравнению с единицей, можно представить
результативную деформацию при изменении длины от l0 до ln как
сумму последовательных малых относительных деформаций 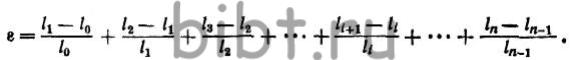
Обозначая через x переменную в пределах от l0 до ln длину отрезка,
li+1- li= dx —
бесконечно малое приращение длины, следуя теории пределов, получим
окончательно выражение относительной конечной деформации: 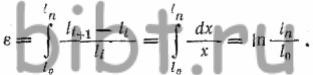 (1)
(1)
Пример 1. Пусть в какой-либо зоне
деформируемой заготовки получено двойное удлинение, а в другой зоне
— двойное укорочение. Тогда: ![]() — приращение, отнесенное к первоначальной длине;
— приращение, отнесенное к первоначальной длине;
![]() — приращение, отнесенное к измеренной длине;
— приращение, отнесенное к измеренной длине;
![]()
![]() - приращение, отнесенное к первоначальной длине;
- приращение, отнесенное к первоначальной длине;
![]() — приращение, отнесенное к измененной длине;
— приращение, отнесенное к измененной длине;
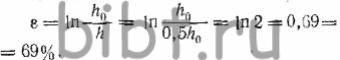
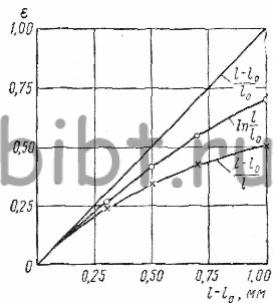
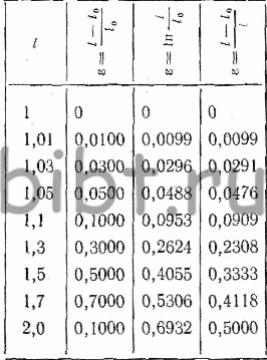
Рис. 1. Относительные деформации, вычисленные по трем формулам (см. табл. 1)
Табл. 1. Приращение отрезка l0= 1 мм и значения относительных деформаций
Отсюда следует, что в том и другом случае формула для конечных деформаций дает одно и то же значение относительной деформации.
Пример 2. Первоначальному отрезку l0= 1 мм дается ряд последовательных приращений. Результаты расчета значений относительных деформаций по трем формулам сведены в табл. 1.
На рис. 1 показаны относительные деформации (табл. 1), вычисленные по трем формулам. При деформации порядка 10% начинается расхождение кривых, достигающее при окончательном значении деформации значительной величины. В пределах до 10% все три формулы дают почти одно и то же численное значение деформации; при деформациях свыше 10% истинное значение относительной деформации отражает расчетная формула (1).
При рассмотрении абсолютной и относительной деформаций предполагалось, что рассматриваемые материальные точки, смещаясь друг относительно друга в процессе деформации, продолжали оставаться на прямой линии. Такой случай может, например, иметь место, если рассматривать смещение материальных точек, расположенных на оси деформируемого образца при его растяжении.
Однако в самом общем случае, в том числе при формоизменяющих и разделительных операциях штамповки, отрезки прямых, соединяющих данные две точки, могут иметь какой угодно наклон к геометрическим осям и направлениям приложенных к заготовке деформирующих сил. Для простоты изучения деформации выбирают материальную точку М и рассматривают смещение относительно нее материальных точек, расположенных на равных от нее расстояниях r0 по всему объему малой сферы. В процессе деформации будет деформироваться и рассматриваемая малая материальная сфера. Относительные смещения на ее поверхности материальных точек выразятся как в изменении их расстояний от центральной точки М, т. е. в удлинении или укорочении соответствующих радиусов малой сферы, так и в повороте этих радиусов в пространстве.
Пусть X, Y, Z — координаты материальной точки М тела до деформации и X + dX, Y + dY, Z + dZ — координаты материальной точки М', расположенной на поверхности сферы весьма малого радиуса r0 с центром в точке М.
Пусть далее х, у, z и х + dx, у + dy, z + dz — координаты тех же материальных точек М и М' в рассматриваемом теле в данной стадии его деформации.
Поскольку каждой совокупности значений координат х, у, z, соответствует вполне определенная совокупность значений координат X, Y, Z, можно три последние рассматривать как непрерывные функции от координат х, у, z. Полагая, что точка М' находится на достаточно малом расстоянии от точки М (радиус r0 элементарной сферы может быть выбран сколь угодно малым), можно написать:
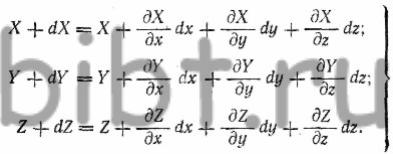 (2)
(2)
Но поскольку до деформации материальная
точка М находилась на расстоянии r от материальной точки М',![]() имеем
и в силу равенств (2) получаем
имеем
и в силу равенств (2) получаем 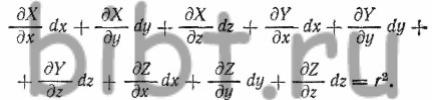 (3)
(3)
Как видно из равенства (3), данное геометрическое место точек представляет собой поверхность второго порядка, все точки которой расположены на достаточно малом расстоянии друг от друга и образуют в своей совокупности не что иное как поверхность эллипсоида. Следовательно, в результате любого вида и любой интенсивности происшедшего в теле формоизменения все материальные точки, располагавшиеся до деформации тела на поверхности малой сферы, разместятся на поверхности малого эллипсоида, в который преобразовалась данная малая сфера.
Направление главных осей деформации рассматриваемой частицы определяется по направлению главных осей малого эллипсоида, преобразованного деформацией из малой сферы.
Обозначая l=> b => h длины трех главных осей эллипсоида, преобразованного деформацией из малой сферы малого радиуса r0, получим выражение трех главных деформаний:
![]() — главный компонент деформации в направлении
наибольшего удлинения;
— главный компонент деформации в направлении
наибольшего удлинения;
![]() — главный компонент деформации в направлении
наибольшего укорочения;
— главный компонент деформации в направлении
наибольшего укорочения;
![]() — средний главный компонент деформации.
— средний главный компонент деформации.
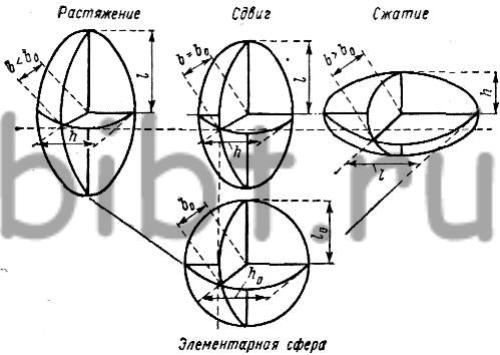
Рис. 2. Основные формопреобразования сферы в эллипсоид
При пластическом формоизменении ε1 всегда положителен, ε3 всегда отрицателен, а ε2 может быть положителен или отрицателен.
Во всех случаях ε1=>ε2=>ε3.
В зависимости от изменения средней главной оси b получается ряд возможных формопреобразований сферы в эллипсоид. Начинаясь от растяжения вдоль оси l при укорочениях вдоль осей b и h, эти формообразования проходят через сдвиг при растяжении вдоль оси l, равном укорочению вдоль оси h и при отсутствии изменения b, заканчиваются сжатием вдоль оси h при удлинениях вдоль осей l и b (рис. 2).
Интенсивность деформации или обобщенная итоговая деформация определяется выражением:
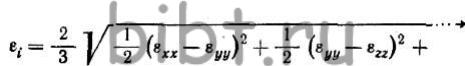
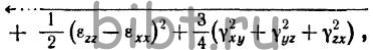 или
или 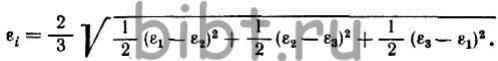 (4)
(4)
Деформация или преобразованный в эллипсоид мысленно выделенный объем малой сферы деформируемого тела находится в прямой зависимости от характера и интенсивности возникших в нем внутренних сил сопротивления. Действующие силы предполагаются расположенными сплошь по всей поверхности объема. Отношение приложенных сил в пределе к бесконечно малой площадке служит показателем интенсивности действующих сил и называется напряжением. Величина вектора напряжения и его направленность меняются вместе с изменением ориентации площадки. Принято называть проекцию на нормаль к площадке наклонного вектора напряжения нормальным компонентом напряжения или нормальным напряжением σ , а проекцию этого вектора на саму площадку — касательным напряжением.
Подобно трем главным осям деформации существуют три взаимно перпендикулярные оси, пересекающиеся в центре исследуемого объема, характерные тем, что на площадках, перпендикулярных этим трем осям, действуют только нормальные напряжения либо напряжения отсутствуют вовсе.
Эти три оси называются главными осями напряжений, три площадки — главными площадками, а три приложенных к ним нормальных напряжения — главными напряжениями. Алгебраически наибольшее из трех главных напряжений σ1, алгебраически среднее σ2 и алгебраически наименьшее σ3:σ1=>σ2=>σ3.
Опыт показывает, что интенсивность
пластического изменения формы тела зависит от разностей величин
главных напряжений, а интенсивность изменения объема — от суммы
всех трех главных компонентов напряжений. Поэтому мысленно выделенная
малая сфера получит одно и то же изменение объема независимо от того,
будут ли к ней приложены три главных напряжения σ1,σ2,σ3 или
соответственно три равных усредненных напряжения, определяемые как их
среднее арифметическое. Эту систему трех равных по величине и по
знаку главных напряжений можно уподобить системе сил, вызывающих
равное всестороннее сжатие или всестороннее растяжение, называемой
гидростатическим давлением р (положительным или отрицательным) 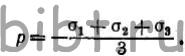 (5)
(5)
Положительное гидростатическое давление вызывает уменьшение объема тела, а отрицательное — увеличение объема.
В основу определения видов напряженно-деформированного состояния положен принцип соответствия вида деформации виду напряженного состояния.
Напряженное состояние называется
растяжением, когда разность (σ2-σ3) мала по сравнению с разностью ![]() ,
сдвигом, когда абсолютная величина разности
,
сдвигом, когда абсолютная величина разности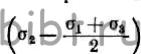 мала по сравнению с разностью (σ1-σ3),
и сжатием, когда разность (σ1-σ2) мала по сравнению с разностью
мала по сравнению с разностью (σ1-σ3),
и сжатием, когда разность (σ1-σ2) мала по сравнению с разностью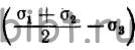 .
.
При простом растяжении σ2=σ3; при линейном растяжении σ2=σ3=0.
При простом сжатии σ1=σ2 ≠0; при линейном сжатии σ1=σ2 =0.
При любом напряженно-деформированном
состоянии его вид определяется из выражения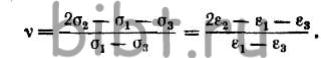
При простом и линейном растяжении v=-1; при простом и линейном сжатии v =+1; при сдвиге v=0.
Количественно напряженное состояние
определяется выражением 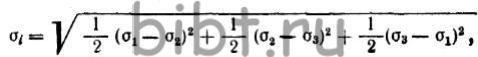 (6) характеризующим интенсивность напряжений.
(6) характеризующим интенсивность напряжений.
Выражение интенсивности напряжений после элементарных алгебраических преобразований принимает вид:
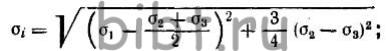 (7)
(7)
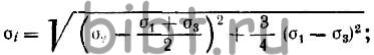 (7*)
(7*)
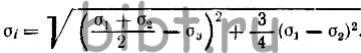 (7**)
(7**)
Выражение интенсивности напряженного состояния апроксимируется линейными относительно главных напряжений зависимостями.
При растяжении второй член подкоренного
выражения правой части равенства (7) заведомо мал по сравнению с
первым, следовательно ![]() (7а)
(7а)
При сдвиге первый член подкоренного выражения правой части равенства (7*) мал по сравнению со вторым; следовательно
![]() (7а*)
(7а*)
При сжатии второй член подкоренного
выражения правой части равенства (7**) мал по сравнению с первым,
следовательно ![]() (7а**)
(7а**)
Граница между видами напряженного состояния соответствует тем значениям главных напряжений, при которых с равной степенью приближения апроксимируется выражение (6) интенсивности напряжений линейными выражениями (7а), (7а*), (7а**).
Граница между растяжением и сдвигом
определяется выражением ![]()
Заметив, что 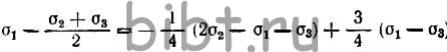 и разделив обе части равенства на (σ1-σ3), имеем
и разделив обе части равенства на (σ1-σ3), имеем 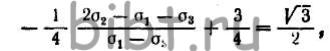 откуда
откуда 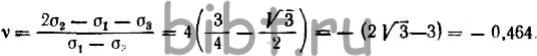
Аналогично устанавливается граница между сдвигом и сжатием. Поэтому напряженное состояние считается растяжением, если -1,0≤v≤-0,464, сдвигом, если —0,464 <v< + 0,464, сжатием, если +0,464 <v<+1,0.