Адрес этой страницы' ?>

Предыдущая Оглавление книги Следующая

2. Связь напряжений и деформаций.

Как известно, связь между напряженным и деформированным состояниями рассматриваемой частицы тела в упругой зоне формоизменения устанавливается равенствами обобщенного закона Гука:
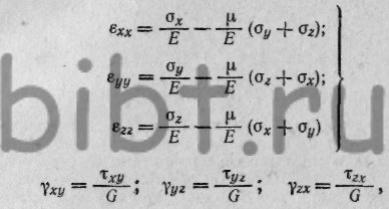(8)

где ε_xx;ε_yy;ε_zz;γ_xy;γ_yz;γ_zx— компоненты относительных деформаций удлинений, укорочений или сдвигов по отношению к принятой системе прямоугольных координат; σ_x;σ_y;σ_z;τ_xy;τ_yz;τ_zx — компоненты нормальных и касательных напряжений относительно той же системы координат; E—модуль Юнга; μ— коэффициент Пуассона; — модуль упругости второго рода или модуль сдвига.

Система равенств (8) путем алгебраических преобразований может быть приведена к эквивалентной системе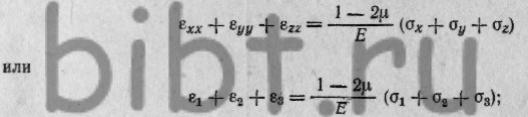

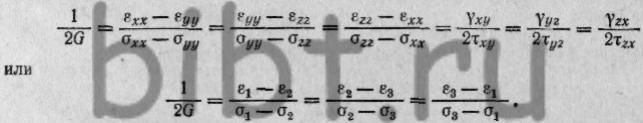
Если подставить значение разностей в уравнение (4) и принять во внимание равенство (6), то при условии идеальной упругости материала получим или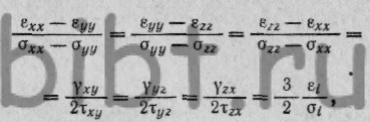 где коэффициент пропорциональности — вполне определенная константа для любого данного вещества.

Характерное отличие пластической зоны формоизменения от упругой состоит в том, что коэффициент пропорциональности являющийся в упругой зоне определенной константой, в пластической зоне за счет деформационного упрочнения становится переменным и различным для различных частиц пластически деформируемого тела.

В условиях малых пластических деформаций при простом нагружении интенсивность напряженного состояния σ_i связана с величиной σ_i однозначной функциональной зависимостью σ_i=Φ(ε_i).

Эта функциональная зависимость, различная для различных материалов, устанавливается экспериментально на основании результатов испытания любого данного материала на простое растяжение либо определяется различными аппроксимирующими зависимостями, например, (9)

Однако в самом общем случае пластического формоизменения, в основном конечного (значительного), и, в частности, при обработке металлов давлением главные оси напряжений могут не совпадать с главными осями деформаций, вид напряженного состояния может не соответствовать виду деформации, а характер нагружения не может быть отнесен к категории простого, так как вследствие значительного формоизменения координаты точек приложения внешних сил изменяются во времени.Поэтому в общем случае пластического формоизменения отсутствует гарантия однозначности протекания процесса деформации или, как это принято называть, монотонность процесса, и непосредственно связь деформаций с напряжениями установить невозможно. В этом случае устанавливается связь напряжений со скоростью деформации. Скоростью деформации или компонентом скорости деформации называется относительная деформация прямолинейного отрезка l в направлении координатных осей, происходящая в течение весьма малого промежутка времени,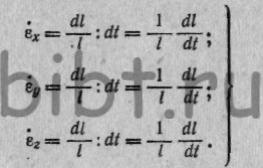 (10)

Три взаимно перпендикулярных направления, вдоль которых в данный момент происходит деформация (наиболее быстрое удлинение в окрестности точки М, наиболее быстрое укорочение и третье, промежуточное между первыми двумя), носят название главных осей скорости деформации, а компоненты скорости деформации, соответствующие этим трем направлениям, — главных компонентов скорости деформации.

Как показывает опыт, при значительном пластическом формоизменении, когда вполне приемлем принцип несжимаемости (относительное изменение объема пластически деформируемой частицы пренебрежимо мало по сравнению с относительными изменениями ее линейных размеров), главные оси напряженного состояния частицы совпадают с главными осями скорости деформации. При этом предполагается, что направление действия наибольшего главного напряжения всегда совпадает с направлением наиболее быстрого удлинения материального волокна, а направление алгебраически наименьшего главного напряжения — с направлением наиболее быстрого укорочения.

Следующее допущение состоит в том, что разности главных напряжений пропорциональны соответствующим разностям главных компонентов скорости деформации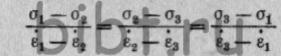 (11) или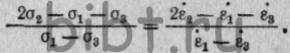

Путем алгебраических преобразований как следствие равенств (11), (6), (4) получаем выражение, количественно устанавливающее скорость изменения интенсивности деформации формы рассматриваемой частицы 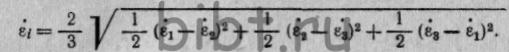(12)

Связь главных напряжений с главными компонентами деформаций выражается: 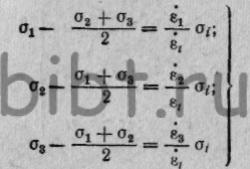(13)
или при обозначении (5): 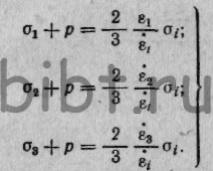(14)

В литературе [11] сформулированы два характерных условия однозначности, монотонности протекания деформации материальной частицы физического вещества: условие совпадения главных осей скорости деформации с одними и теми же материальными волокнами частицы и условие неизменности за весь процесс вида малой деформации, происходящей при переходе в текущую стадию из предшествующей, весьма близкой. При этом процесс конечной деформации рассматривается как совокупность последовательных малых деформаций, фиксируемых в данные рассматриваемые отрезки времени как его промежуточные «текущие» стадии.

Согласно первому условию монотонности процесса материальное волокно, претерпевающее в любой рассматриваемой стадии пластической деформации частицы, например, наиболее быстрое удлинение, должно было наиболее быстро удлиниться (а следовательно, наиболее удлиниться) за весь предшествующий процесс деформации. Следовательно, при монотонном процессе направление наиболее быстрого удлинения материального волокна (первая главная ось скорости деформации) всегда совпадает с направлением его наибольшего результативного (суммарного за весь предшествующий процесс) удлинения (т. е. с первой главной осью результативной деформации), а следовательно, и с первой главной осью напряженного состояния.

Аналогично, третья главная ось скорости деформации совпадает как с третьей главной осью результативной деформации, так и с третьей главной осью напряжений и т. д.

Согласно рассматриваемому принципу монотонного протекания процесса деформации, главные компоненты результативной деформации (логарифмической деформации) должны быть пропорциональны соответствующим главным компонентам скорости деформации, т. е. 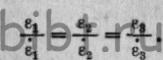(15)

Принимая во внимание выражения (12) и (1), можно равенства (15) привести к виду откуда 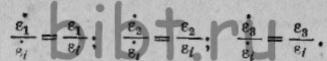(16)

Для случая монотонности протекания процесса деформации из равенств (14) с учетом равенств (16) получаем; 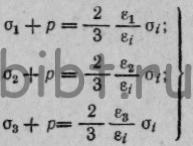(17)
или с учетом выражения (5) 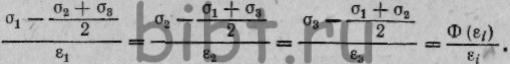(18)

Из анализа уравнения (18) видно, что если какие-либо два напряжения равны (например,σ₁=σ₂), то равны и соответствующие деформации (ε₁=ε₂). Если деформация в одном направлении отсутствует (например,ε₁=0), то напряжение в направлении отсутствующей деформации равно полусумме двух других напряжений, т. е. (19) что является необходимым условием плоского деформированного состояния.

Предыдущая Оглавление книги Следующая