Адрес этой страницы' ?>

Предыдущая Оглавление книги Следующая

Операции вытяжки. Напряженно-деформированное состояние плоской заготовки при вытяжке.

Процесс деформации плоской заготовки в зоне фланца при вытяжке немонотонный, так как наблюдается знакопеременность компонентов скорости деформации материальных частиц.

При втягивании плоской заготовки в вытяжную матрицу в ее центральной зоне возникает деформация утонения, вызванная двусторонним растяжением материала дна. При движении пуансона в глубь матрицы остальная масса металла заготовки

подвергается интенсивному формоизменению. Периферийные слои металла подвергаются значительному сжатию в тангенциальном направлении и удлинению во всех направлениях, перпендикулярных тангенциальному. Поэтому материал периферийных толщине слоев в начале процесса вытяжки увеличивается, а затем по мере приближения их к пуансону уменьшается до величины зазора между пуансоном и матрицей, что свидетельствует об изменении знака компонента скорости деформации в направлении нормали к плоскости заготовки.

Напряженно-деформированное состояние отдельных участков заготовки в процессе вытяжки показано на рис. 7. Участок фланца имеет напряженное состояние плоское, а деформированное — объемное. Деформация происходит в направлении толщины заготовки (ε_n), в радиальном (ε_ρ) и тангенциальном (ε_θ) направлениях.


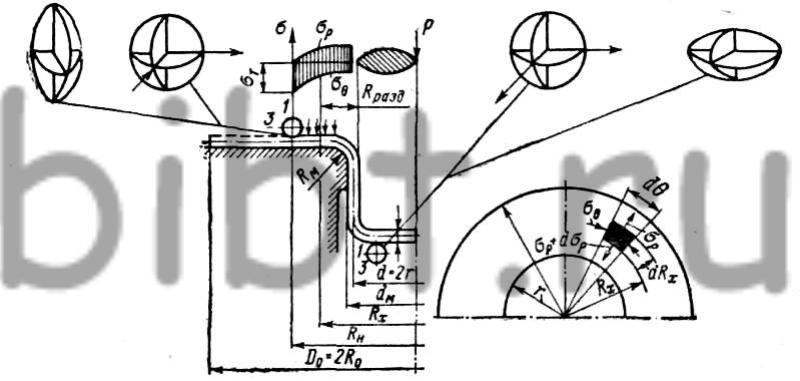
Рис. 7. Напряженно-деформированное состояние плоской заготовки при вытяжке: 1, 3 —главные оси деформации; главная ось 2 (на рисунке не показана) проектируется в точку

Максимальной по абсолютному значению является деформация ε_θ, неравномерная по фланцу при переходе его в полость матрицы. Волокна заготовки, расположенные на расстоянии R_x от оси симметрии, подвергаются при переходе в стенку детали деформации

Волокна материала фланца(R_x=R₀) подвергаются наибольшей деформации, где m=d/D — коэффициент вытяжки.

Чем меньше абсолютное значение т, тем больше деформации во фланце.

Участки заготовки, расположенные вблизи полости матрицы, деформируются в тангенциальном направлении незначительно, а при R_x = r деформация ε_θ=0.

Соотношение между деформациями ε_θ и ε_ρ зависит от соотношения соответствующих напряжений. Как следует из эпюры распределения напряжений σ_ρи σ_θ (рис. 7) на фланце наблюдаются две зоны:

1) периферийная от R_разд (т. е. радиуса, разделяющего зоны утолщения и утонения заготовки) до R_н; здесь — положительна и, следовательно, толщина заготовки увеличивается;

2) внутренняя зона от r до R_разд где а ε_n— отрицательна и толщина заготовки уменьшается. На радиусе R_разд напряжение -σ_θ = σ_ρ и, следовательно, -ε_θ =ε_ρ, а ε_n=0, т. е. толщина заготовки здесь не изменяется. Граница R_разд определяется из условия равенства выражений (47) и (48), при решении которых R_разд=0,61R_н.

В вертикальной стенке напряженное состояние — линейное, а деформированное — плоское. Деформация в тангенциальном направлении мала и ею практически пренебрегают. На закруглениях матрицы и пуансона заготовка испытывает сложное напряженно-деформированное состояние, обусловливаемое ее дополнительным изгибом.

Величина и соотношение напряжений σ_θ и σ_ρ заготовки в зоне фланца при условии, что толщина заготовки в процессе вытяжки не изменяется и остается равной исходной толщине S, определяются решением двух уравнений: уравнения равновесия сил, действующих на выделенный элемент (рис. 7), и уравнения пластичности.

Уравнение равновесия (43)

Учитывая, что для малых углов и упрощая выражение (43), получаем (44)

Уравнение пластичности (45) При решении уравнений (44) и (45) получаем (46)

Интегрируя выражение (46) и определяя постоянную интегрирования из условия, что на свободной кромке заготовки при R_x=R_н напряжение σ_ρ=0, получим (47)

Тангенциальное напряжение σ_θ определяется из уравнения пластичности (45):

(48)

Из анализа уравнений (47) и (48) следует, что напряжение σ_ρ изменяется от нуля до максимального в зоне перехода в вертикальную стенку (R_x=r) и равно (49)

При этом максимальное значение напряжения в радиальном направлении неодинаково в различных стадиях процесса. При R_н=R₀, т. е. при начальном моменте операции, σ_{ρ max} имеет наибольшее значение (50)

Степень деформации материальной частицы, расположенной на торце периферийной зоны заготовки, за весь немонотонный процесс формоизменения, равняющийся сумме интенсивностей главных логарифмических деформаций ε_θ; ε_ρ, ε_z (практически двух монотонных периодов), значительно выше степени деформации частицы, расположенной в донной части заготовки. При этом вид напряженно-деформированного состояния материальной частицы в первом периоде — сжатие, во втором периоде при R₀=r — сдвиг.

Тем не менее, как установлено опытом, опасность разрушения в процессе вытяжки донной части больше, чем торцевой. Объясняется это тем, что в донной части при вытяжке всегда возникают более жесткие схемы напряженного состояния чем в торцевой.

Действительно, в первом периоде на материал торцевой части заготовки действуют напряжения Коэффициент жесткости схемы напряженного состояния определяется из выражения

т. е. схема напряженного состояния достаточно мягкая. В донной части заготовки σ₁=σ₂; σ₃=0, т. е.

Следовательно, схема напряженного состояния донной части более жесткая.