
| Главная |
| Поиск по сайту |
Адрес этой страницы' ?>
Предыдущая Оглавление книги Следующая
Операции гибки. Схема напряженно-деформированного состояния заготовки при гибке.
При гибке в разных слоях заготовки возникают деформации и напряжения, разные по знакам: вблизи наружной (выпуклой) поверхности размеры элементарной материальной частицы увеличиваются в тангенциальном направлении и уменьшаются в радиальном, а вблизи внутренней (вогнутой) поверхности они уменьшаются в тангенциальном направлении и увеличиваются в радиальном. Поэтому изгибаемый лист разделяют по толщине на две зоны: на зону, где материальные волокна удлиняются в тангенциальном направлении, и зону, где они укорачиваются в тангенциальном направлении. Радиус границы этих двух зон называют радиусом нейтрального слоя.
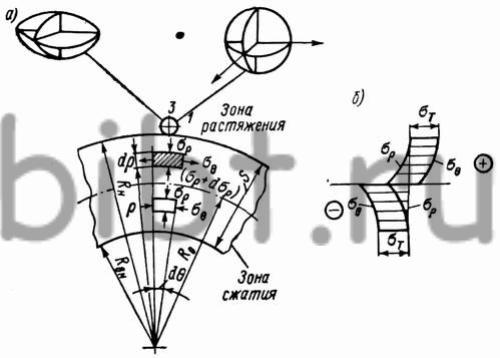
Рис. 6. Схема напряженно-деформированного состояния заготовки: а — при гибке; б — распределение напряжений по высоте сечения заготовки
Соответственно деформациям возникают тангенциальные напряжения, радиальные напряжения, которые появляются вследствие давления продольных волокон металла друг на друга, а также аксиальные напряжения, обусловленные отсутствием деформаций вдоль оси при гибке заготовки, за исключением участков у торца заготовки длиной меньше толщины листа.
Напряженно-деформированное состояние заготовки при гибке показано на рис. 6 и наглядно иллюстрирует объемное напряженное и плоское деформированное состояния. Напряжения σθ и σρ являются крайними и главными, а σz— средним главным напряжением.
С учетом упрощающих допущений, удовлетворяющих требованиям практики, распределение напряжений по очагу деформаций можно определить совместным решением уравнений равновесия и пластичности.
Уравнение
равновесия для заштрихованного элемента определяется проектированием
действующих на него сил на радиус R0 и
приравниванием их суммы нулю ![]() (33)
(33)
Уравнение пластичности при условии, что σθ и σρ являются крайними главными напряжениями для данного напряженного состояния, будет иметь следующий вид:
σθ- σρ=βσT. (34)
Ввиду плоского деформированного состояния коэффициент β, учитывающий влияние среднего главного напряжения σz, будет равен 1,155.
Подставив значение σθ из
уравнения (34) в (33) с учетом знаков напряжений, получим ![]() (35) откуда
(35) откуда ![]() (36)
(36)
После интегрирования получим ![]() (37)
(37)
Постоянная с интегрирования
определяется из условия, что если ρ=Rн, то σρ=0,
т. е.![]()
Тогда радиальные напряжения ![]() (38)
(38)
Подставляя значение σρ в
уравнение пластичности, получим выражение для определения
тангенциальных напряжений ![]() (39)
(39)
Среднее главное напряжение σz (аксиальное) для плоскодеформированного состояния в соответствии с
уравнением (28) определим из уравнения ![]()
Аналогичным путем определяются
уравнения для напряжений σρ и σθ в
сжатой зоне:![]() (40)
(40) ![]() (41)
(41)
Из анализа уравнения (38) следует, что радиальные напряжения σρ на внешних растянутых (ρ=Rн) и на внешних сжатых (ρ=Rвн) слоях равны нулю. Максимальное значение они принимают на нейтральном слое, когда ρ=R0.
Характер распределения тангенциальных напряжений σθ в растянутой и сжатой зонах различен. В растянутой зоне при ρ=R0 σθ=σθmin.
При ρ=Rн σθ = σθ max=σT; в сжатой зоне при ρ=R0 σθ = σθ max.
При ρ=Rвн σθ = σθ min =σT.
Видом напряженно-деформированного
состояния наружных и внутренних слоев заготовки является сдвиг, так
как при условии несжимаемости ε1=-ε3, ε2=θ, v=0, 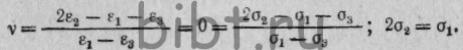
Коэффициент
П жесткости схемы будет 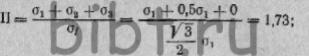
![]()
Опыт подтверждает, что разрушение
материальных волокон на гибочных операциях штамповки происходит при ![]() что
объясняется более жесткой схемой (П = 1,73) по сравнению с линейным
напряженным состоянием (П = 1).
что
объясняется более жесткой схемой (П = 1,73) по сравнению с линейным
напряженным состоянием (П = 1).
Распределение напряжений по высоте
сечения изогнутой заготовки показано на рис. 6, а. Хорошо видно, что
в растянутой зоне по всей высоте сечения напряжения![]() меньше
предела текучести, а в сжатой зоне — больше предела текучести.
Такое соотношение напряжений обусловливает смещение нейтрального слоя
от срединной поверхности в сторону сжатой зоны (к центру кривизны). В
результате этого растяжение будет действовать на большей части
сечения, чем сжатие, так как только в этом случае будет выполнено
условие статики и сумма сил, действующих в растянутой зоне, будет
равна сумме сил, действующих в сжатой зоне.
меньше
предела текучести, а в сжатой зоне — больше предела текучести.
Такое соотношение напряжений обусловливает смещение нейтрального слоя
от срединной поверхности в сторону сжатой зоны (к центру кривизны). В
результате этого растяжение будет действовать на большей части
сечения, чем сжатие, так как только в этом случае будет выполнено
условие статики и сумма сил, действующих в растянутой зоне, будет
равна сумме сил, действующих в сжатой зоне.
Смещение нейтрального слоя от среднего
по сечению слоя можно определить аналитическим способом из условия,
что на нейтральном слое радиальные напряжения![]() определяемые
уравнениями (38) и (40), должны быть одинаковые. Из этого условия
определяется радиус нейтрального слоя R0. В результате решения этих уравнений получаем
определяемые
уравнениями (38) и (40), должны быть одинаковые. Из этого условия
определяется радиус нейтрального слоя R0. В результате решения этих уравнений получаем ![]() (42)
(42)
Радиус среднего слоя определяется
выражением ![]()
Относительное смещение нейтрального
слоя от срединной поверхности заготовки получим из равенства ![]() или в относительных радиусах
или в относительных радиусах![]() получим
получим ![]()
Расчеты, подтверждаемые практикой,
показывают, что чем меньше внутренний относительный радиус, тем
больше смещается нейтральный слой от срединного положения в сторону
центра радиуса кривизны. При ![]() =
3 смещение составляет примерно 3%; при
=
3 смещение составляет примерно 3%; при ![]() =
0,5 — около 12%.
=
0,5 — около 12%.