Адрес этой страницы' ?>

Предыдущая Оглавление книги Следующая

Условия пластичности. . Элементарный тетраэдр, грани которого совпадают с главными плоскостями.

Условия пластичности устанавливают соотношения между действующими напряжениями, при которых металл переходит из упругого состояния в пластическое. При линейном одноосном напряженном состоянии этот переход происходит, когда действующее напряжение достигает напряжения предела текучести σ_T. В случае сложного напряженного состояния (плоского или объемного) число возможных комбинаций значений действующих напряжений, вызывающих переход упругих деформаций металла в пластические, может быть бесконечно велико. Эти возможные комбинации определяются уравнениями пластичности, которые выводятся на основании экспериментальной проверки принятых гипотез и определяют связи между напряжениями и деформациями при заданных температурно-скоростных параметрах.

В обработке металлов давлением при анализе напряженно-деформированного состояния заготовок в разных операциях наибольшее распространение получили условия постоянства максимальных касательных напряжений и условие постоянства удельной энергии формоизменения.

Первое условие — постоянство максимальных касательных напряжений формулируется следующим образом: пластическое состояние наступает тогда, когда какое-либо одно из трех главных касательных напряжений достигает вполне определенной величины, равной половине напряжения текучести металла при линейном напряженном состоянии. Эта гипотеза основана на том, что на поверхности заготовки с развитием пластической деформации появляются линии скольжения в направлениях действия главных касательных напряжений. Поэтому естественно предположить, что пластическое деформирование наступает тогда, когда главные касательные напряжения достигают экстремальных значений, которые зависят только от свойств деформируемого металла и не зависят от характера напряженного состояния.

Второе условие — энергетическая гипотеза утверждает, что переход деформируемого металла в пластическое состояние происходит независимо от схемы напряженного состояния тогда, когда потенциальная энергия формоизменения, отнесенная к единице объема, достигает некоторой величины, зависящей только от свойств деформируемого металла.

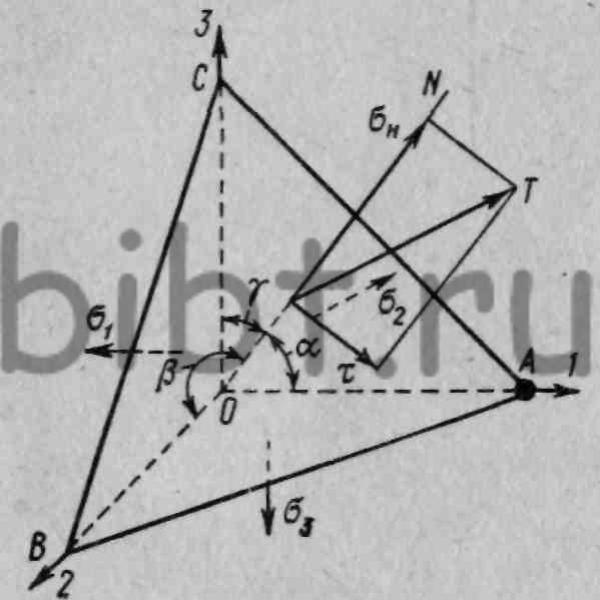
Рис. 4. Элементарный тетраэдр, грани которого совпадают с главными плоскостями

Рассмотрим выделенный в деформируемом геле элементарный объем, ограниченный тремя гранями (ВОС, АОС и АОВ), совпадающими с главными плоскостями, и четвертой произвольно ориентированной гранью ABC (рис. 4). На трех гранях полученного тетраэдра будут действовать главные напряжения σ₁;σ₂;σ₃, а на четвертой грани будет действовать полное напряжение T имеющее нормальную и касательную составляющие σ_н и τ.

Обозначим косинусы углов, образующие нормаль N к произвольно ориентированной грани ABC с главными осями 1, 2, 3, через cos α= cos(N;1)=a₁; cos β = cos(N;2)=a₂; cos γ=cos(N;3)=a₃.

Эти косинусы являются направляющими относительно грани ABC, а соотношение их между собой определяется известным из аналитической геометрии уравнением (23)

Из условия равновесия сил на гранях тетраэдра нормальное σ_н и касательное τ напряжения на грани ABC выражаются следующими уравнениями: 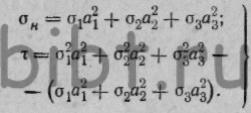(24)

Из уравнения (23) Тогда:

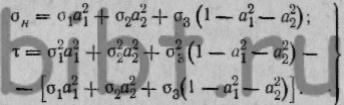(25)

Для определения положения грани с максимальным по величине касательным напряжением уравнение (25) следует продифференцировать по a₁ и a₂ и полученные первые производные приравнять нулю. Анализ показывает, что максимальные или главные касательные напряжения действуют на гранях, проходящих через одну координатную ось и делящих угол между двумя другими осями пополам, т. е. наклоненных к двум координатным плоскостям под углом 45°:

Подстановка этих значений косинусов в уравнение (24) дает

(26)

Для других граней получим аналогичные выражения:

(27)

(28)

Здесь τ₁;τ₂;τ₃— максимальные или главные касательные напряжения.

При линейном напряженном состоянии (когда σ₂=σ₃) переходов пластическое состояние совершается при следующем соотношении:

Как было указано выше, условие постоянства максимальных касательных напряжений не зависит от схемы напряженного состояния, поэтому в окончательном виде это условие с учетом уравнений (26)—(28) можно записать так:

Для перехода от упругих деформаций к пластическим достаточно выполнение одного из этих трех равенств.

При плоском напряженном состоянии (σ₂=0) условие пластичности выражается уравнением σ₁-σ₃ = ±σ_T, где σ₁= σ_max, σ₃ = σ_min и имеется в виду, что σ₂=σ_ср =0 (среднее главное напряжение). Если σ₂=0 не среднее, а одно из крайних напряжений, то уравнение пластичности изменяется. Тогда в зависимости от соотношений главных напряжений уравнения пластичности для плоского напряженного состояния имеют вид: 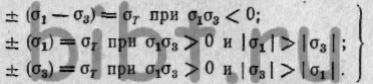(29)

Первое уравнение используется тогда, когда напряжения σ₁ и σ₃ имеют разные знаки, а последние два — когда эти напряжения имеют одинаковые знаки. Согласно энергетической гипотезе 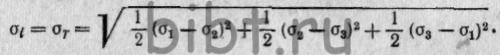(30)

При σ₂=σ₁ (σ₁=σ_max) или при σ₂=σ₃ (σ₃=σ_min) из уравнения (29)

следует, что ±(σ₁-σ₃)=σ_T.

Если положить что является условием плоского деформированного состояния (ε₂=0) [см. уравнения (13) и (17)], то из выражения (30) получим

В результате уравнение (30) можно в упрощенной форме представить в виде
±(σ₁ -σ₃)=βσ_T, (31)

где коэффициент β учитывает влияние среднего главного напряжения σ₂ и может изменяться в пределах 1,0—1,15. Максимальное значение коэффициента β имеет место при плоском деформированном состоянии, когда видом напряженно-деформированного состояния является сдвиг.

Уравнением (31) можно пользоваться и для плоского напряженного состояния. Однако в этом случае следует иметь в виду, что если σ₂=0 не является средним напряжением, то условие пластичности выражается как

Оба условия пластичности — условие постоянства главных касательных напряжений и энергетическое условие — совпадают при линейном напряженном состоянии (σ₂=σ₃=0), при объемном напряженном состоянии, когда среднее главное напряжение равно одному из крайних напряжений ( σ₂=σ₁ или σ₂= σ₃) а также при плоском напряженном состоянии, когда оба напряжения равны между собой ( σ₁= σ₃).