Адрес этой страницы' ?>

Предыдущая Оглавление книги Следующая

Уравнения равновесия. Напряженное состояние элементарного объема.

Уравнения равновесия выражают условия равновесия выделяемой из объема деформируемого тела частицы в форме прямоугольного параллелепипеда с ребрами, параллельными координатным осям (рис. 3, а).

Изменение напряжений на параллельных гранях, отстоящих от точки О на величину половины длины ребер δ_x;δ_y;δ_z, будет выражаться частным дифференциалом по координате, вдоль которой переместилась грань. Например, на грани параллелепипеда, внешняя нормаль к которой совпадает с положительным направлением оси ОХ, компоненты напряженного состояния определятся выражениями: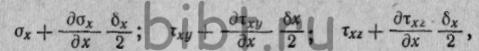 где— 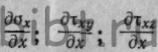значения в точке О частных производных компонентов напряженного состояния по координате X;

δ_x/2 — расстояние геометрического центра рассматриваемой грани от точки О.

Если предположить, что выделенный параллелепипед должен находиться в равновесии, то равнодействующая всех сил, действующих на граничную поверхность параллелепипеда, т. е. на шесть его граней, должна быть равна нулю. Следовательно, нулю должны быть равны и три ее проекции на координатные оси, т. е.

(20) и два аналогичных равенства.

Окончательно условие равновесия параллелепипеда выразится тремя уравнениями: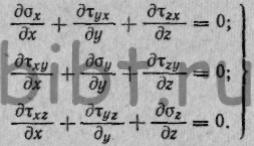 (21)

Поскольку выделенная частица должна находиться в равновесии, то и моменты действующих на нее сил также должны равняться нулю. Отсюда следует, что пар ные касательные напряжения равны друг другу (τ_xy=τ_yx; τ_yz=τ_zy; τ_zx=τ_xz) и поэтому уравнения (21) содержат шесть неизвестных напряжений (три нормальных и три касательных) и задача статически неопределима.

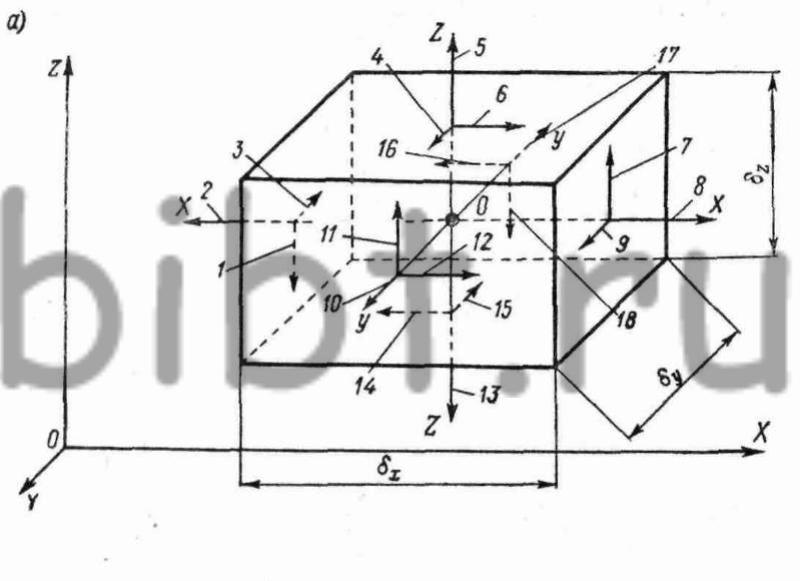
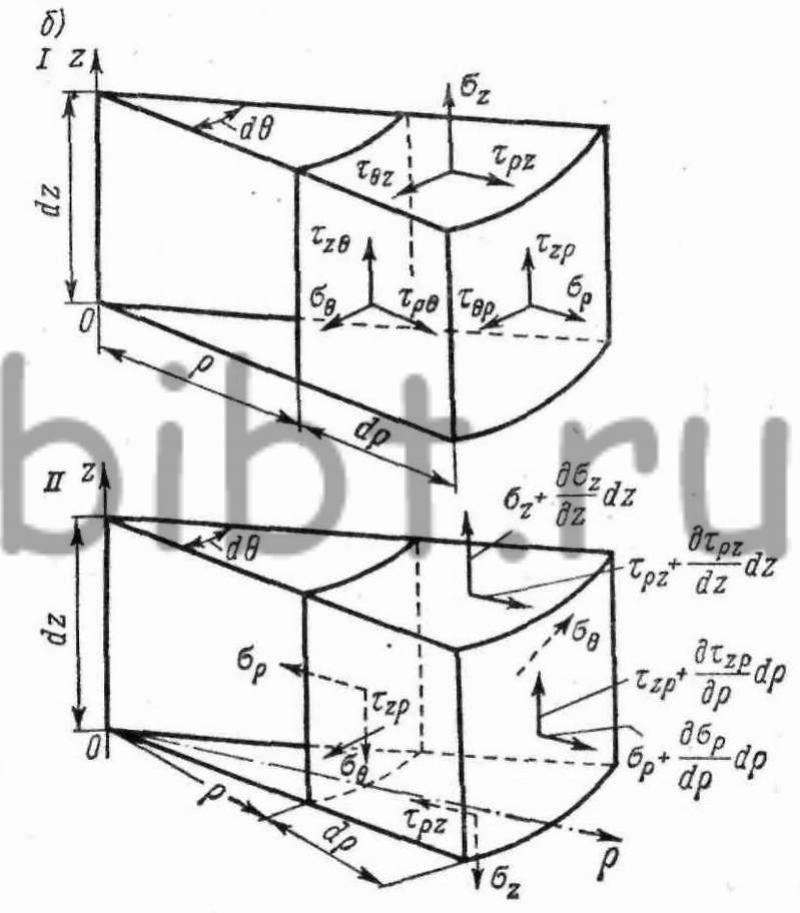
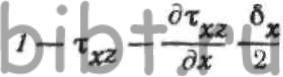
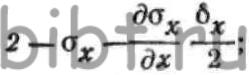
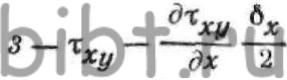
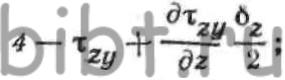
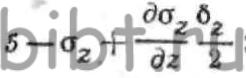
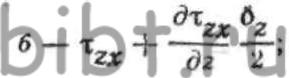
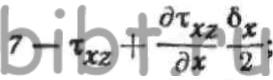
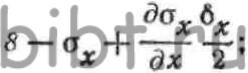
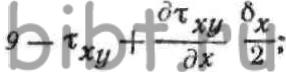
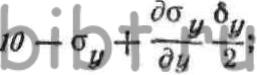
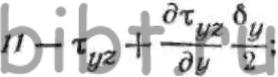
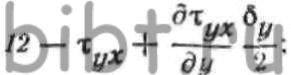
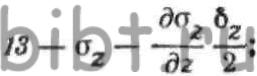
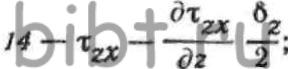
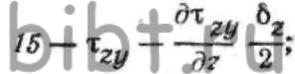
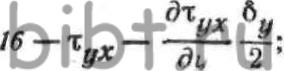
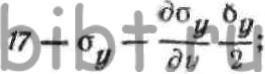
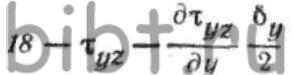
Рис. 3. Напряженное состояние элементарного объема: а — в прямоугольных координатах; б — в цилиндрических координатах. I — общий случай; II — при осесимметричном деформировании;

При штамповке деталей, имеющих форму тел вращения, полагают, что деформирование происходит с сохранением осевой симметрии нагрузки, т. е. напряжения и деформации будут одинаковыми во всех меридиональных сечениях, являющихся главными плоскостями напряженно-деформированного состояния. В этом случае удобнее пользоваться цилиндрической системой координат, где положение точки определяется радиус-вектором ρ, полярным углом θ и аппликатой z (рис. 3, б)

Выделим элементарный объем из тела вращения двумя меридиональными, двумя окружными сечениями и двумя разными по высоте сечениями. Нормальные и касательные напряжения на гранях этого объема будут изменяться только вдоль осей ρ и z и не будут зависеть от угла θ. Вследствие осевой симметрии внешних нагрузок на гранях, расположенных на меридиональных сечениях, касательные напряжения τ_θz и τ_ρθ равны нулю. Тогда в силу парности будут равны нулю и касательные напряжения τ_zθ и τ_ρθ . Следовательно, при осесимметричном деформировании на рассматриваемый элементарный объем действуют три (σ_θ; σ_ρ; σ_z) нормальных напряжения и дваτ_zρ и τ_ρz равных касательных напряжения (рис. 3, б).

Проектируя силы на оси ρ и z, получим условия равновесия в виде двух уравнений:

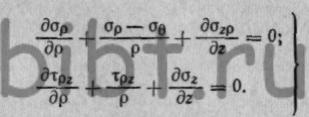(22)

При листовой штамповке можно принять, что напряженное состояние заготовки плоское (σ_z=0), и тогда для осесимметричного деформирования решение задачи упрощается. При этих допущениях 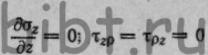и условие равновесия (22) выразится одним дифференциальным уравнением в обыкновенных производных (напряжения в том случае изменяются только в зависимости от радиус-вектора ρ). В полярной системе координат это уравнение примет вид (22*)

Уравнение (22*) широко используется для анализа напряженно-деформированного состояния заготовок при операциях вытяжки гибки, раздачи и др., когда детали имеют форму тел вращения.