
| Главная |
| Поиск по сайту |
Адрес этой страницы' ?>
<<Предыдущая страница Оглавление книги Следующая страница>>Точная установка и выверка деталей на универсальном дели-тельно-поворотном столе с пересекающимися осями.
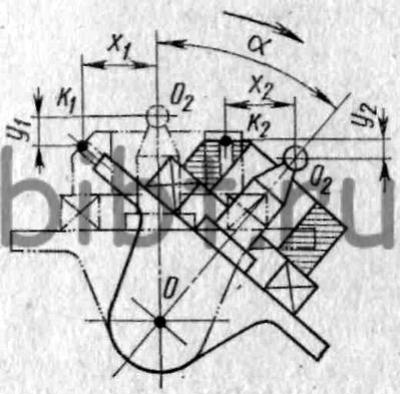
Рис. 128. Схема установки детали на универсальном делительно-поворотном столе с пересекающимися осями для обработки плоскости и отверстия под углом к оси планшайбы:
О — ось наклона планшайбы. O2 — центр шарового наконечника центрирующего стержня, x1, y1 — размеры точки K1 относительно центра O2 до поворота планшайбы, х2, y2 — размеры до точки K2, занявшей новое место относительно центра O2 после поворота планшайбы на угол α
На рис. 128 показана схема установки детали на универсальном делительно-поворотном столе с пересекающимися осями для фрезерования плоскости и сверления отверстия под углом к оси детали. Для выверки стола и оси обрабатываемой детали относительно оси шпинделя используется центрирующий стержень с шаровым наконечником. Пунктиром показано исходное положение стола и обрабатываемой детали. Контурными линиями показано положение стола и обрабатываемой детали после их поворота на угол α относительно оси О в позицию обработки.
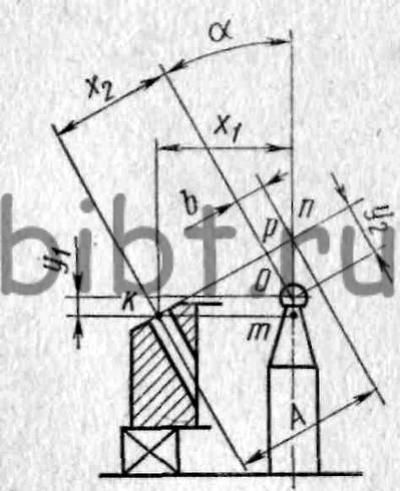
Рис. 129. Расчетная схема для определения координат обработки плоскости и отверстия под углом к оси планшайбы при установке детали на поворотном столе с пересекающимися осями
На рис. 129 дана расчетная схема для случая, рассмотренного на рис. 128. Координаты центра отверстия x1 и y1 обозначены относительно центра шарового наконечника центрирующего стержня. Эти размеры заданы требованиями чертежа. Следует определить размер х2, который является координатой отверстия относительно центра шарового наконечника после поворота стола на угол α.
Из расчетной схемы видно, что отрезок х2 представляет собой разность отрезков А и b: х2=А-b.
Рассмотрим треугольник nKm. В этом треугольнике угол nKm = α, гипотенуза nK=А, а катет Km = x1, откуда следует, что A= x1 / cos α
Противолежащий углу α катет mn можно выразить: mn = x1tgα. Если рассмотрим малый треугольник nop, увидим, что его гипотенузу on можно выразить как разность отрезков mn-mo, но mn = x1tgα, a mo=y1, поэтому on= x1 tgα-y1.
В малом треугольнике угол nop = α, а противолежащим катетом является отрезок b, следовательно, b = on sin α = [x1 tg α - y1] sin α.
Подставляя полученные значения А и b в формулу х2, получим х2 = (x1 / cos α) - (x1 tgα -y1) sin α
Чтобы это выражение упростить, раскроем скобку и сделаем преобразования
х2= (x1/cos α) - x1 tgα sin α + y1 sinα выразим tg α через sin α / cos α , х2= (x1/cos α) -(x1sinα * sin α)/cos α +(y1 sinα); сложим два первых дробных выражения, одновременно вынесем за скобки x1 : x 2 = x1 ((1-sin2 α)/cos α) + y1 sin α; известно, что sin2α + cos2α= 1, следовательно, 1-sin2α =cos2α. Сделав соответствующую подстановку в числителе и сократив на cos α, окончательно получим x2=x1cosα+ y1sin α.
Если кроме сверления отверстия необходимо точно профрезеровать наклонную плоскость, то нужно определить размер y2. Гипотенуза малого треугольника on = x1tg α-y1; умножив это выражение на cos α, получим искомую величину y2=(x1tg α- y1)*cos α.
Пример. Для детали, изображенной на рис. 128, требуется определить координаты отверстий х2 и размер до плоскости скоса y2
Исходные данные: x1=45 мм; y1 = 6 мм; α = 30°.
Из таблиц тригонометрических функций находим: sin 30°=0,5, cos 30°=0,866, tg 30° = 0,5774.
Решение. Воспользуемся окончательными формулами х2 и y2: x2 = x1cosα+ y1sinα = 45 × 0,866 + 6 × 0,5 = 41,97 мм; у2 = (х1 tg α - y1 cos α = (45 × 0,5774 - 6) × 0,866 = 17,635278 мм.
В зависимости от того, какое место занимают координаты центра отверстия или обрабатываемой плоскости (выше центра шарового наконечника, ниже центра, справа или слева), изменяется вид формулы, по которой следует рассчитывать координаты. В этом можно убедиться, расположив точку, для которой отыскиваются координаты, в другом квадранте. В литературе, предназначенной для работающих на координатно-расточных станках, приводятся, схемы расчета и готовые формулы применительно к различным случаям определения координат.