Адрес этой страницы' ?>

Точная установка и выверка деталей на универсальном делительно-поворотном столе с непересекающимися осями.

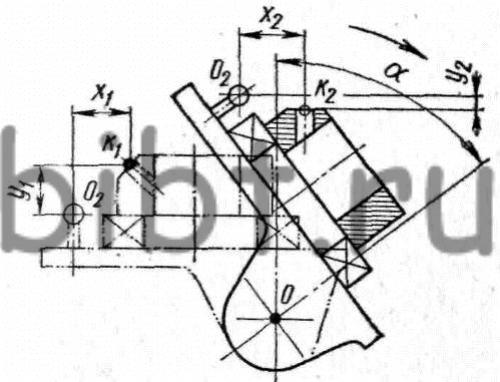
Рис. 130. Схема установки детали на универсальном делительно-поворотном столе с непересекающимися осями для обработки плоскости и отверстия под углом к оси планшайбы: О — ось наклона планшайбы, O₂ — ось центрирующего пальца, х₁, y₁ — координаты точки К₁ относительно оси O₂ до наклона планшайбы, x₂, y₂ —координаты точки K₂ относительно оси O₂ после наклона оси планшайбы на угол α

На рис. 130 дана схема установки детали на универсальном делительно-поворотном столе с непересекающимися осями. На этом столе в качестве базы для отсчета координат используется центрирующий палец, положение оси которого O₂ точно выверено относительно оси поворота стола О. Размеры, определяющие расстояние пальца до оси поворота, обозначены на таблице, прикрепленной к корпусу стола.

Штрихпунктирными линиями изображено начальное положение стола и детали. Центр обрабатываемого отверстия К₁ задан координатами x₁ и y₁ относительно оси центрирующего пальца О₂. Найдем новые координаты х₂ и y₂ для центра отверстия К₂ после поворота стола и детали на угол α по часовой стрелке.

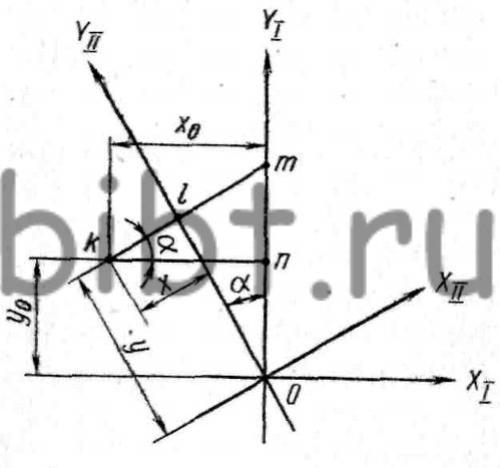
Рис. 131. Расчетная схема для определения координат обработки плоскости и отверстия под углом к оси планшайбы при установке детали на поворотном столе с непересекающимися осями

Чтобы приступить к расчетам, составим расчетную схему (рис. 131). Центр отверстия К первоначально занимал положение относительно осей ординат X_I, и Y_I, определенное координатами х₀ и y₀. После того как стол с деталью повернулся по часовой стрелке на угол α, точка K изменила свое положение. Она приблизилась к оси ординат и удалилась от оси абсцисс.

Сохранив центр отверстия K на прежнем месте, повернем оси ординат на угол α против часовой стрелки, обозначив это новое положение осей Х_II и Y_II а новые координаты центра К через х и у.

Выразим новые координаты через начальные значения x₀ и y₀ и соответствующие тригонометрические функции угла α.

Рассмотрим два треугольника olm и mKn. Отрезок x=Km-lm; Km в треугольнике mKn является гипотенузой, а прилежащий к углу nKm катет Kn равен х₀. Таким образом, можно написать:

Km = x₀ / cos α . Отрезок lm является противолежащим катетом угла α в треугольнике lom; lm / om = sin α, но om = on+mn. Отрезок on равен y₀, а mn находится из треугольника mKn : mn = x₀ tg α.

Минус перед ординатой 35,862 говорит о том, что мы на схеме (см. рис. 130) имеем изображение, не соответствующее углу поворота 20°. В нашем случае ось пальца по вертикали относительно центра отверстия должна располагаться не выше, а ниже на 35,862 мм. Чтобы избежать ошибок, следует тщательно составлять схемы расчетов, а также обращать внимание на знаки перед числами.

В книге «Работа на координатно-расточных станках» (см. литературу в конце книги) приводятся готовые формулы и числовые примеры для случаев обработки самых различных деталей. Обработка пространственно сложных деталей на универсальных поворотно-делительных столах описана в указанной литературе. Примеры, приведенные в этой главе, дают представление о методике расчетов и приемах по точной выверке и установке деталей на универсальных поворотно-делительных столах. Усвоение этих сведений позволит самостоятельно решать многие задачи, возникающие в заводской практике.