Адрес этой страницы' ?>

<<Предыдущая страница Оглавление книги Следующая страница>>

Деформация изгиба. Осевой момент сопротивления изгиба.

Если брус находится под действием двух пар сил (см. рис. 228,д), расположенных в плоскости его продольной оси, то возникает деформация изгиба. При деформации изгиба часть волокон удлиняется, а часть становится короче. Между зонами растяжения и сжатия располагается нейтральный слой.

В нейтральном слое волокна не подвергаются деформации и сохраняют свою длину неизменной. Чем дальше волокна расположены от нейтрального слоя, тем большую деформацию они испытывают.

Таким образом, при изгибе в поперечных сечениях бруса под действием внутренних сил возникают нормальные напряжения растяжения и сжатия, и их величина зависит от положения точки в сечении. Наибольшие напряжения возникают в наиболее удаленных точках от нейтральной оси. Эти напряжения в зоне растяжения обозначаются +σ_max, а в зоне сжатия -σ_max.

В точках, расположенных на нейтральной осп, напряжения равны нулю. Это простейший вид изгиба под действием пары сил. Но изгиб может возникнуть и при ином нагружении бруса, например под действием сил и реакций, перпендикулярных оси балки. В таких случаях для определения внутренних силовых факторов применяют метод поперечных сечений.

Рассмотрим (рис. 230, а) любое сечение, например I-I. Рассечем брус, отбросим левую часть и рассмотрим равновесие оставшейся (рис. 230,б). Для равновесия требуется соблюдение трех условий. Первое условие - равенство нулю суммы сил, направленных параллельно оси У. Это условие дает Q=R_в. Второе условие - равенство нулю суммы сил, наравленных параллельно оси X, соблюдается тождественно, так как обе силы, и внешняя и равнодействующая внутренних сил, направлены перпендикулярно этой оси.

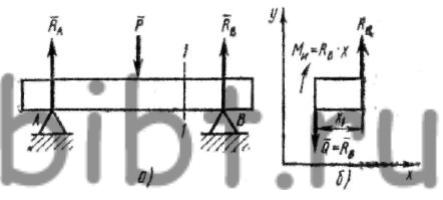
Рис. 230. Изгиб под действием силы и реакций:

а - схема бруса, б - схема равновесия правой части бруса

Соблюдение третьего условия - равенство нулю суммы моментов всех сил - подсказывает нам, что в сечении должны дополнительно действовать внутренние силы, приводящие к образованию пары сил, т. е. изгибающего момента M_и=R_вХ₁. Таким образом выясняется, что в сечении действуют такие силовые факторы: поперечная сила и изгибающий момент. Первый - это следствие деформации сдвига, а второй - следствие деформации изгиба. Однако, как показала практика, главную опасность для прочности материала при поперечном изгибе представляют нормальные напряжения, поэтому в дальнейшем при рассмотрении подобных случаев мы не будем учитывать внутренних касательных сил.

Выше мы отмечали, что чем дальше от нейтрального слоя расположены в брусе волокна, тем больше они деформируются, а следовательно, и большее оказывают сопротивление деформации. Сопротивление деформации зависит не только от размеров поперечного сечения бруса, но и от ориентации его по отношению к изгибающей силе.

Итак, поскольку основное сопротивление изгибу оказывают периферийные слои материала, при изгибе целесообразно применять брусья с сечениями, в которых материал расположен дальше от нейтральной оси. Так, при одной и той же площади применение кольцевого сечения (трубы) целесообразнее применения сплошного; прямоугольные выгоднее квадратного, причем рациональней большее отношение высоты к ширине. Наиболее выгодными являются специальные профили: двутавры, швеллеры.

Учитывая, что по закону Гука напряжение в каждой точке деформируемого поперечного сечения пропорционально относительной деформации, а сама относительная деформация пропорциональна расстоянию точки от нейтральной оси, можно с помощью математических преобразований, приравняв сумму моментов внутренних сил внешнему моменту (метод сечения), определить величину максимальных напряжений изгиба, т. е.

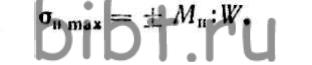
Сам вывод не приводится ввиду его сложности.

Знаки «±» означают, что в точках, наиболее удаленных от нейтральной оси но расположенных по разные стороны от нее, будут различные по характеру деформации нормальные напряжения: в одном случае напряжения растяжения, в другом - напряжения сжатия.

Величина W (см. выше) называется осевым моментом сопротивления изгиба. Она характеризует способность поперечного сечения сопротивляться деформации изгиба относительно нейтральной оси.

Величина W зависит от формы и размеров поперечного сечения, а также от его ориентации по отношению к изгибающей силе. Для фиксации последнего к обозначению добавляют индекс, соответствующий обозначению нейтральной оси, например W_z или W_y. Размерность W - м³, см³, мм³.

Для квадратного сечения со стороной а W_z=W_y=a³:6.

Для прямоугольного сечения с размерами b и h W_z=bh²:6 и W_y =hb²:6.

Для специальных сечений типа двутавров и швеллеров величины осевых моментов сопротивления изгибу приводятся в справочниках.

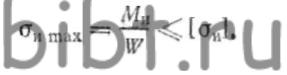
При проектных расчетах определяют минимальные размеры опасного поперечного сечения, которые при заданной нагрузке обеспечат прочность. Для этого используют формулу M_и:W≤[σ_и], затем находят осевой момент по формуле W≥М_и:[σ_и] и по вышеприведенным формулам рассчитывают необходимые размеры поперечного сечения.

При проверочных расчетах определяют максимальные действительные напряжения, т. е. напряжения в наиболее опасных точках опасного сечения и сравнивают их с допускаемыми. В этом случае предварительно находят изгибающий момент в опасном сечении и допускаемые напряжения